Abstract:
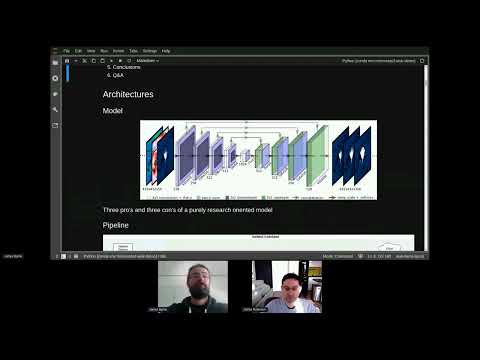
Many schemes proposed for standardisation in the ongoing NIST post-quantum cryptography process are in the area of lattice-based cryptography. In addition to its potential use in a post-quantum world, lattice-based cryptography has become popular due to its wide applicability, with a key application being Fully Homomorphic Encryption (FHE). In this talk we consider FHE schemes based on the Ring Learning with Errors (Ring-LWE) problem and focus on two matters of practical interest. The first is the selection of secure Ring-LWE parameters. In particular, we discuss the differing estimates used in the submissions to the NIST process for the running time of algorithms to solve Ring-LWE. The second is the choice of an appropriate encoding from raw data into the plaintext space, which can impact on efficiency. We discuss a variant of the Fan-Vercauteren FHE scheme which gives a plaintext space that is very convenient for encoding and enables the homomorphic evaluation of circuits with a higher depth.
This talk is based on the following joint works:
1. with Albrecht, Curtis, Deo, Davidson, Postlethwaite, Virdia, Wunderer: Estimate all the {LWE, NTRU} schemes! https://estimate-all-the-lwe-ntru-schemes.github.io/docs/
2. with Chen, Laine, Xia: High-Precision Arithmetic in Homomorphic Encryption: https://eprint.iacr.org/2017/809
Add comment